Access the Code of Practice online

This registration will be required once-only per browser/device, which is achieved using a cookie stored on your device.

There is no password required, and your information will not be shared with any third parties.

Please register and accept the terms for the NZMRM online COP

First Name *

Last Name *

Email *

Accept Terms

By ticking this box you confirm that you have read and accept the Terms listed below

Disclaimer

Although the information contained in this Code has been obtained from sources believed to be reliable, New Zealand Metal Roofing Manufacturers Inc. makes no warranties or representations of any kind (express or implied) regarding the accuracy, adequacy, currency or completeness of the information, or that it is suitable for the intended use.

Compliance with this Code does not guarantee immunity from breach of any statutory requirements, the New Zealand Building Code or relevant Standards. The final responsibility for the correct design and specification rests with the designer and for its satisfactory execution with the contractor.

While most data have been compiled from case histories, trade experience and testing, small changes in the environment can produce marked differences in performance. The decision to use a particular material, and in what manner, is made at your own risk. The use of a particular material and method may, therefore, need to be modified to its intended end use and environment.

New Zealand Metal Roofing Manufacturers Inc., its directors, officers or employees shall not be responsible for any direct, indirect or special loss or damage arising from, as a consequence of, use of or reliance upon any information contained in this Code.

New Zealand Metal Roofing Manufacturers Inc. expressly disclaims any liability which is based on or arises out of the information or any errors, omissions or misstatements.

If reprinted, reproduced or used in any form, the New Zealand Metal Roofing Manufacturers Inc. (NZMRM) should be acknowledged as the source of information.

You should always refer to the current online Code of Practicefor the most recent updates on information contained in this Code.

Scope

This Code of Practice provides requirements, information and guidelines, to the Building Consent Authorities, the Building Certifier, Specifier, Designer, Licensed Building Practitioner, Trade Trainee, Installer and the end user on the design, installation, performance, and transportation of all metal roof and wall cladding used in New Zealand.

The calculations and the details contained in this Code of Practice provide a means of complying with the performance provisions of the NZBC and the requirements of the Health and Safety at Work Act 2015.

The scope of this document includes all buildings covered by NZS 3604, AS/NZS 1170 and those designed and built under specific engineering design.

It has been written and compiled from proven performance and cites a standard of acceptable practice agreed between manufacturers and roofing contractors.

The drawings and requirements contained in this Code illustrate acceptable trade practice, but recommended or better trade practice is also quoted as being a preferred alternative.

Because the environment and wind categories vary throughout New Zealand, acceptable trade practice must be altered accordingly; in severe environments and high wind design load categories, the requirements of the NZBC will only be met by using specific detailing as described in this Code.

The purpose of this Code of Practice is to present both Acceptable Trade Practice and Recommended Trade Practice, in a user-friendly format to ensure that the roof and wall cladding, flashings, drainage accessories, and fastenings will:

comply with the requirements of B1, B2, E1 E2 and E3 of the NZBC;
comply with the design loading requirements of AS/NZS 1170 and NZS 3604 and with AS/NZS 1562;
have and optimised lifespan; and
be weathertight.

COP v24.12:Useful-Information;

Useful Information

18 Useful Information

Useful tools and tables to do calculations and conversions for roof and wall cladding. Just choose the correct online caculator, input your values, and get the answer.

Conversion Factors

18.1 Conversion Factors

Label for Single Option

18.1A Measurement Conversions

To convert from this	into this To convert this back	multiply by this divide by this
atmosphere	millibar	1013.25
atmosphere	pascal	101.325
cubic foot	cubic metre	0.028317
cubic inch	cubic millimetre	16387.1
cubic yard	cubic metre	0.764555
foot	metre	0.3048
foot per minute	metre per minute	0.3048
foot per minute	metre per second	0.00508
foot per second	metre per second	0.3048
foot pound force per second	watt	1.35582
gallon (Imp)	litre	4.54609
gallon (US)	litre	3.78541
inch	metre	0.0254
inch	millimetre	25.4
inch mercury	kilopascal	3.38638
inch water gauge	kilopascal	0.248642
kilogram	kN	102
kilometre per hour	knot	0.539
knot	kilometre per hour	1.852
knot	nautical mile/h	1
knot	ft/h	6080
knot	metre per second	0.515
metre Head of water	kPa	9.8
mile	kilometre	1.609344
mile per hour	kilometre per hour	1.609344
millimetre mercury	kilopascal	0.133322
millimetre water gauge	pascal	9.78904
MPa	kip	6.895
ounce	gram	28.3495
ounce per square foot	gram per square metre	305.152
ounce per square yard	gram per square metre	33.9057
pound	kilogram	0.45359237
pound force	newton	4.44822
pound force foot	newton.metre	1.35582
pound force inch	newton.metre	0.112985
pound force per square foot	kilopascal	0.0479
pound force per square inch	bar	0.69
pound force per square inch	pascal	6894.76
pound force per square inch	kilopascal	6.89476
pound force per square inch	megapascal	0.006895
pound per cubic foot	kilogram per cubic metre	16.0185
pound per foot	kilogram per metre	1.48816
pound per square foot	kilogram per square metre	4.882
square foot	square metre	0.092903
square foot per ton	square metre per tonne	0.091436
square inch	square millimetre	645.16
square mile	square kilometre	2.59
square yard	square metre	0.836127
Steel thickness in mm	Weight of steel kgs/m²	7.85
ton	tonne	1.01605
ton force foot	kilonewton metre	3.03703
ton force per square inch	megapascal	15.4443
ton per cubic yard	tonne per cubic metre	1.32894
ton, freight (40 ft³)	cubic metre	1.13267
yard	kilometre	0.000914

Water 0 ̊ – 100 ̊ increases in volume by 4.4%
1 litre    = 1 kg = 0.001 m3
1 m3      = 1000 litres
Weight of steel kgs/m2   = thickness in mm x 7.85
1 kN   = 102 kg
1 kip     = 6.895 MPa

Pitch & Rise Calculator

18.2 Pitch & Rise Calculator

The relationship between the pitch, fall or rise and the horizontal, is the relationship between the opposite and the adjacent sides of a right angled triangle.

This is known as the tangent of the angle. (tan ɸ) with the opposite side being the rise and the adjacent side the horizontal distance.

Enter any two values on the illustration for live calculations.

Rafter Length (Hypotenuse)

Angle ɸ°

Rise (Opposite)

Span (Adjacent)

Fall1 in

18.2A Rafter, Hip and Rise Chart

Pitch	Rafter length	Hip/Valley Length	Vertical Rise	Valley Angle
	per metre span	per metre span	per metre span
0.5	1.000	1.414	0.009	179°
1	1.000	1.414	0.017	179°
1.5	1.000	1.414	0.026	178°
2	1.001	1.415	0.035	177°
3	1.001	1.415	0.052	176°
4	1.002	1.416	0.070	174°
5	1.004	1.417	0.087	173°
6	1.006	1.418	0.105	172°
7	1.008	1.420	0.123	170°
8	1.010	1.421	0.141	169°
9	1.012	1.423	0.158	167°
10	1.015	1.425	0.176	166°
11	1.019	1.428	0.194	164°
12	1.022	1.430	0.213	163°
13	1.026	1.433	0.231	162°
14	1.031	1.436	0.249	160°
15	1.035	1.439	0.268	159°
16	1.040	1.443	0.287	158°
17	1.046	1.447	0.306	156°
18	1.051	1.451	0.325	155°
19	1.058	1.456	0.344	153°
20	1.064	1.460	0.364	152°
21	1.071	1.465	0.384	151°
22	1.079	1.471	0.404	149°
23	1.086	1.477	0.424	148°
24	1.095	1.483	0.445	147°
25	1.103	1.489	0.466	145°
26	1.113	1.496	0.488	144°
27	1.122	1.503	0.510	143°
28	1.133	1.511	0.532	141°
29	1.143	1.519	0.564	140°
30	1.155	1.528	0.577	139°
31	1.167	1.537	0.601	137°
32	1.179	1.546	0.625	136°
33	1.192	1.556	0.649	135°
34	1.206	1.567	0.675	133°
35	1.221	1.578	0.700	132°
36	1.236	1.590	0.727	131°
37	1.252	1.602	0.754	130°
38	1.269	1.616	0.781	128°
39	1.287	1.630	0.810	127°
40	1.305	1.644	0.839	126°
41	1.325	1.660	0.869	125°
42	1.346	1.677	0.900	124°
43	1.367	1.694	0.933	122°
44	1.390	1.712	0.966	121°
45	1.414	1.732	1.000	120°
46	1.440	1.753	1.036	119°
47	1.466	1.775	1.072	118°
48	1.494	1.798	1.111	117°
49	1.524	1.823	1.15	115°
50	1.556	1.849	1.192	114°
51	1.589	1.877	1.235	113°
52	1.624	1.907	1.280	112°
53	1.662	1.939	1.327	111°
54	1.701	1.973	1.376	110°
55	1.743	2.010	1.428	109°
56	1.788	2.049	1.483	108°
57	1.836	2.091	1.540	107°
58	1.887	2.136	1.600	106°
59	1.942	2.184	1.664	105°
60	2.000	2.236	1.732	104°
65	2.366	2.569	2.145	100°
70	2.924	3.09	2.747	97°
75	3.864	3.991	3.732	94°
80	5.759	5.845	5.671	92°

Material Density, Melting Point, Expansion And Modulus

18.3 Material Density, Melting Point, Expansion And Modulus

18.3A Density, Melting Point, Expansion and Young Modulus

Material	Density kg/m³	Melting point °C	Expansion mm/10m/100°C	Youngs modulus Gpa
Air	1.29
Air acetylene		2500*
Aluminium, rolled	2710	658	24	69
Brass	8330	900	18
Carbon Dioxide 0°C	1.99
Cement	1281
Concrete, reinforced 2% steel	2420
Copper	8938	1083	17	131
Glass	2787	850	9
Gold	19290	1063	14
Hydrogen 0°C	0.0897
Helium 0°C	0.178
Ice	913	0
Iron, cast	7208	1530	12	179
Lead, rolled	11325	327	29	16
Nitrogen 0°C	1.25
Oxygen 0°C	1.43
Oxy acetylene		4400*
Pinus Radiata	609			6
Polycarbonate	1244	133	64
Polyester	1299	245	80&num;
P.V.C.	1465	86	140
Silver	10500	960	19
Silver solder		735
Easy-flo		630
Solder Lead 50%	9302	210
(Eutectic) Lead 33%/tin 67%	8615	180
Snow: fresh	96	1
wet compact	320
Stainless Steel 304	8080	1425	17	193
Stainless Steel 316	8080	1385	16	193
Steel, low carbon	7850	1350	12	200
Tin	7280	231	27
Water: fresh 4°C	1000
Water: fresh 20°C	988
Water: fresh 100°C	958
Water: salt	1009-1201
Zinc: rolled	7192	419	29

* max flame temperature
&num; glass reinforced polyester GRP expansion = 22
To convert Centigrade to Farenheit.
To convert Farenheit to Centigrade.
C° = F° - 32° x .56
F° = C° x 1.8 + 32°

Thermal Conductivity K

18.3.1 Thermal Conductivity K

18.3.1A Thermal Conductivity

Material	W/mK
Copper	385
Aluminium	205
Zinc	108
Steel	50
Lead	35
Stainless Steel	16
Ice	2
Glass	1	.05
Concrete		0.94
Brick		0.8
Water (20°C)		0.56
Timber (Pine)		0.14
Snow		0.1
Kraft building paper		0.07
Fibreglass		0.035
Rockwool		0.035
Polystyrene		0.035
Air (20°C )		0.025
Polyurethane (Rigidised)		0.016

Decadic Number System

18.4 Decadic Number System

18.4A Decadic Numbers

Symbol	Designation	Long Measure			Multiplier
T	Tera	Billion (Trillion			10¹²
G	Giga	Milliard (Billion USA)			10⁹
M	Mega	Million			10⁶
ma	Myria	Ten thousand	mam	Myriametre	10⁴
k	Kilo	Thousand	km	Kilometre	10³
h	Hecto	Hundred	hm	Hectometre	10²
da	Deca	Ten	dam	Decametre	10
		One	m	Metre	1
d	Deci	Tenth	dm	Decimetre	10^-1
c	Centi	Hundredth	cm	Centimetre	10^-2
m	Milli	Thousandth	mm	Millimetre	10^-3
μ	Micro	Millionth		Micrometre (Micron)	10^-6
n	Nano	Milliardth	nm	Nanometre	10^-9
p	Pico	Billionth	pm		10^-12

International Symbols

18.4.1 International Symbols

18.4.1A The Greek Alphabet

Upper		Lower		Greek
Α	A	α	a	alpha
Β	B	β	b	beta
Γ	G	γ	g	gamma
Δ	D	δ	d	delta
Ε	E	ε	e	epsilon
Ζ	Z	ζ	z	zeta
Η	H	η	h	eta
Θ	Q	θ	q	theta
Ι	I	ι	i	iota
Κ	K	κ	k	kappa
Λ	L	λ	l	lambda
Μ	M	μ	m	mu
Ν	N	ν	n	nu
Ξ	J	ξ	j	xi
Ο	O	ο	o	omicron
Π	P	π	p	pi
Ρ	R	ρ	r	rho
Σ	S	σ	s	sigma
Τ	T	τ	t	tau
Υ	Y	υ	y	upsilon
Φ	F	φ	f	phi
Χ	X	χ	x	chi
Ψ	C	ψ	c	psi
Ω	V	ω	v	omega

Geometry And Measurement

18.5 Geometry And Measurement

Enter values below for automatic calculations

a= area

b= base

d= diameter

h= height

l= length

r= radius

π= 3.1416

c= circumference = 2πr or 22/7d

Areas

Circle= πr² or 0.7854 d²

Square, rectangle, rhombus or rhomboid= bh

Triangle= .5 bh

Trapezoid= .5 two parallel sides x h

Side of square of area equal to circle= 0.8862 d

Diameter of circle equal in area to square= 1.1284 side of square

Parabola= .66 bh

Ellipse= 0.7854 d1 d2

Area of any figure of four or more unequal sides is found by dividing it into triangles, finding areas of each and adding together.

Surface Area

Cube= 6b²

Sphere= πd²

Lateral surface area of regular figure= .5 cbh (slant height)

Cylinder (Lateral surface area)= πdh

Cylinder (Total surface area)= πdh + 2πr2

Cone (Total surface area)= ab + c of base x .5h (slant height)

Volume

Cube= b³

Sphere= 0.5236 d³

Pyramid= .33 abh

Cone= .33 abh

Cylinder= πr²h

Table of polygons

S= side of polygon.

R= Radius of circumscribed circle.

r= Radius of inscribed circle.

A= Angle formed by the intersection of the sides.

NameNo of sidesAngle

Trigon360°

Pentagon5108°

Hexagon6120°

Octagon8135°

Decagon10144°

Area of any regular polygon = Radius of inscribed circle x 1/2 number of sides x length of one side.

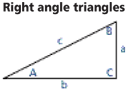
Right Angle Triangles

Enter any two values on the illustration for live calculations.

Hypotenuse

Angle ɸ°

Opposite

Adjacent

Fall1 in

18.5A Triangle Values

FindGiven Solution

A a, b tan A = a / b

a, c sin A = a /c

b, c cos A = b / c

B a, b tan B = b / a

a, c cos B = a / c

b, c sin B = b / c

a A, b b tan A

A, c c sin A

b, c √ c² - b²

b A, a a / tan A

A, c c / cos A

a, c √ c² - a²

c A, a a / sin A

A, b b / cos A

a, b √ a² + b²

Area a, b ab / ²

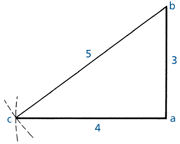
18.5B To Find a Right Angle

Draw a line ab 3x long. At point a scribe an arc 4x long.
At point b scribe an arc 5x long to intersect a c.
Join ac and b, ac and ab are at 900.

Velocities

18.6 Velocities

18.6A Velocity

Unit	m/s	kms/h	mile/h
mile / hour m/s km/h	0.44704 1 0.277778	1.60934 3.6 1	1 2.23694 0.62137

Velocity is the distance travelled in one second (m/s).

The following speeds are approximate and are assumed to be constant and in a straight direction and therefore are also the velocity.

Description marked R are speed records.

18.6B Velocity Comparison

	m/s	km/h	mile/hour	Beaufort Scale
Calm	0	<1	0		Smoke rises vertically
Light Air	0.8	3	2	1	Smoke rises on angle
Man walking	1.5	5.5.	3.5
Light breeze	2.5	9	5.6	2	Feel wind on face
Gentle breeze	4.5	16	10	3	Flags extend
Moderate breeze	7	25	15.5	4	Raises dust
Fresh breeze	10	35	22	5	Trees sway, waves
Runner 100m R	10	35	22
Strong breeze	12.5	45	28	6	Telegraph wires whistle
Racehorse trotting R	15	54	33
Moderate gale	15.5	56	35	7	Difficult to walk
Fresh gale	18.5	67	42	8	Branches break
Racehorse R	19	68	42.5
Ostrich	20	72	45
Racing cyclist R	22	79	49
Strong gale	23	82	51	9	Slight building damage
Whole gale	26.5	96	60	10	Trees uprooted
N.Z. Road speed limit	28	100	62.5
Skier downhill	28	100	62.5
Storm	31	111	69	11	Widespread damage
Low wind speed NZS 3604	32	115	71
Hurricane	33.5	120	75	12	Severe damage
Medium wind speed NZS 3604	37	133	83
High wind speed NZS 3604	44	158	98
AS/NZS 1170	45	162	101
Swift - fastest bird	47	169	105
Very high wind speed NZS 3604	50	180	111
AS/NZS 1170 (Cook Strait)	51	184	114
Moderate cyclone	55	198	153
Tennis serve R	66	238	148
Bullet train (Japan)	69	248	154
Severe tropical cyclone	70	252	157
TGV express train	77	277	172
Wind R	103	371	230
Boeing 747	256	920	572
Sound in air	333	1199	743
Land speed R	341	1228	763
Rotation of earth at equator	465	1674	1040
Concorde	649	2336	1452
303 Bullet	792	2851	1772
Lockheed Blackbird R	981	3529	2193
Moon round the earth	1000	3600	2237
Sound through steel	5100	18360	11408
To escape earth’s gravity	7823	28163	17500
Fastest man has travelled	11176	40234	25000
Earth round the sun	29700	106920	66437
Pioneer space probe	66720	240192	149248
Light and electric waves	299388000	1077614064	669600000	186,000 miles/sec

Cricket Penetration Patterns

18.7 Cricket Penetration Patterns

When cricket and diverter penetration flashings are used, the pitch of the cricket valley will always be less than the pitch of the roof.

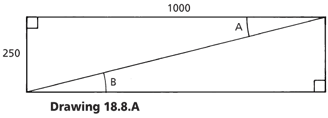
To find the pitch of a roof or valley, a simple method is to use a 1m long level measuring stick and measure the rise as shown in drawing 18.7A Measuring Stick Method. The relationship between the rise and the horizontal distance is known as the tangent of the angle and is calculated by using tan f = O/A (being the opposite side divided by the adjacent side). See 18.2 Pitch & Rise Calculator.

18.7A Measuring Stick Method

250/1000 = 0.25 = 14° (1 in 4)

N.B. Angles A and B are equal.

It is possible to obtain the length of the hypotenuse by using √ a2 + b2

Cricket flashings as described in section 6 can be made to suit any penetration width, any cricket flashing depth to width ratio and roof pitch down to 3°. For simplicity, three angles have been selected.

f X = 45°
f Y = 27°
f Z = 18°

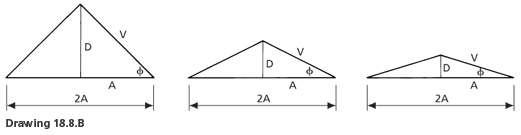
VARIATION OF CRICKET VALLEY DESIGN DEPENDENT ON DEPTH AND ROOF PITCH

Penetration Width = 2A
Depth = D
Valley = V

18.7B Cricket Variations

f X = 45°
D = A
V = √2 = 1.42

f Y = 27°
D = 1/2A
V = √1.25 = 1.118

f Z = 18°
D = 1/3A
V = √1.11 = 1.054

To find the cricket valley pitch when the roof pitch is known, it is necessary to find the depth (D) of the cricket. If the depth of the cricket is half of the width of the penetration, as shown for 'Cricket X' the angles are at 45° and there is a defined relationship between the length of the valley of the cricket and the width of the penetration and also between the pitch of the valley of the cricket and the pitch of the roof.

This is 1 : √ 2 = 1.42, which means that to maintain the desired 3° fall in the cricket valley, the minimum roof pitch (4°) can be calculated using table 15.8.

If the depth of the cricket is a quarter or a sixth of the width of the penetration, there are also defined relationships between the pitch of the valley of the cricket and the pitch of the roof.

These are described in table 18.7C Relationships between the pitch of the valley of the cricket and the pitch of the roof as 'Cricket Y' and 'Cricket Z'.

All figures comply with the minimum fall of 1.5°, but all the bold figures will provide a 3° cricket valley pitch. This methodology is valid for all sizes of penetration. However, there is a point at which, having a design with a wide penetration and a low pitch, it becomes uneconomic to pursue the ideal 3° fall in the cricket valley. When the roof pitch is known, the minimum allowable fall of the cricket valley pitch (1.5°) can then be read from table 15.8.

It is permissible to lower the valley pitch because 1.5° allows sufficient fall to clear debris from the valley and therefore qualifies as a warrantable flashing.

A diverter flashing without a cricket design only shifts the position of the cricket to the top over-flashing of the penetration as shown on drawing 9.7.6B Cricket Flashings, unless the penetration is rotated 45° as shown on drawing 9.7.6C Diverter Flashings.

18.7C Relationships between the pitch of the valley of the cricket and the pitch of the roof

ROOF PITCH	3°	4°	5°	6°	7°	8°	9°	10°
TANGENT	.0524	.0699	.0875	.1051	.1228	.1405	.1584	1763
CRICKET X	2°	3°	3.5°	4.5°				10°
CRICKET Y	1.5°	1.75°	2.25°	2.75°	3.25°	8°	9°	10°
CRICKET Z	n/a	n/a	1.5°	2°	2.25°	2.5°	3°	3.5°

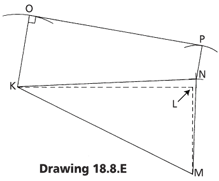
PROCEDURE TO MAKE A HALF PATTERN FOR A CRICKET PENETRATION FLASHING

Example:
A net penetration width is 550 mm wide and gross width to the flat of the pans is 620 mm (2A).
The back curb is required to have a fall of 3°.
The roof pitch is 7°.
From Table 18.7C Relationships between the pitch of the valley of the cricket and the pitch of the roof . select the cricket - Type Y

Given:

Half the width of the cricket
Depth of the Y cricket from drawing 15.8.B (D=1/2A)
Height of the side curb
Height to the top of the cricket
H - Hc = Hr
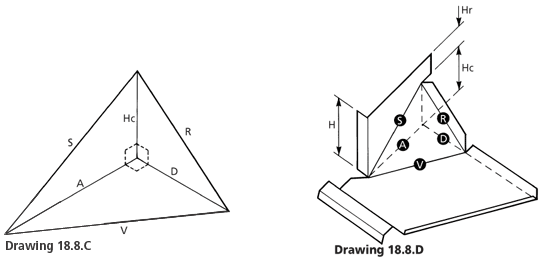
From Drawing 15.8.C
Find the length of V, S and R.
Right angle triangle, therefore, the length of V.

A = 310mm
D = 155mm
H = 130mm
Hc = 70mm
Hr = 60mm

V = √ A2 + D2
A = 346 mm

Right angle triangle, therefore, the length of R.

Right angle triangle, therefore, the length of S.

R = √ Hc² + D²

R = 170 mm

S = √ A² + Hc²

R = 318 mm

18.7D Cricket Pattern

DRAW A HALF PATTERN

1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.

Draw a dotted line K - L length equal to A
From L draw a dotted line at right angles L - M length equal to D
Draw the line K - M (length equal to V)
With centre M scribe an arc length equal to R
With centre K scribe an arc length equal to S
From their point of intersection, N draw a line to K and also to M
With centre K scribe an arc length equal to H.
With centre N scribe an arc length equal to Hr.
Draw a line as a tangent to the two arcs
From point K, draw a line at right angles to intersect this line at O.
From O measure length A to a point P
The shape K-M-N-P-O is the net cricket pattern

18.7E Drawing a Cricket Half-Pattern

18.7F Assembling a Cricket Penetration

Sheet Metal Work For Roofing Contractors.

18.8 Sheet Metal Work For Roofing Contractors.

When forming various flashings in sheet-metal the Roofing Contractor is required to know how to cut the material in order to obtain the desired shape.

Basic knowledge of geometrical drawing and mensuration is required and this section explains the methods which are employed to ensure accurate results.

A straight line. A straight line is a line drawn in the shortest manner between two given points, so any other line between these points is a curved line.

18.8A Parallel Lines

Parallel lines are lines which, when extended, do not touch. Given a line CD, to draw a parallel line set a compass to the required distance apart and with C and D as centres, describe two arcs. A line drawn as a tangent to both arcs will be a parallel line to CD.

18.8B Perpendicular Line

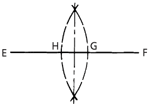
To draw a perpendicular line. Given a straight line EF, set a compass to any distance more than half the distance EF and, with E and F as centres, describe arcs of radius EG and FH.

A line drawn through the points of intersection of these arcs is perpendicular to EF and bisects the distance EF.

18.8C Dividing a line into equal parts

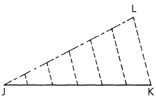
To divide a line into any number of equal parts. Given a straight line J K, draw another line J L at any suitable angle and no particular length. Set off on JL, at any reasonable distance apart, a number of equal spaces similar in number to the parts into which JK is to be divided.

Connect L and K with a line, and parallel to this draw other lines through points on JL. These divide JK into the required number of equal parts.

18.8D Bisecting and Arc

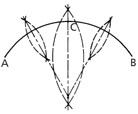
Given an arc AB, set a compass to a distance a little more than half that between the ends and with A and B as centres, describe arcs of equal radii.

A line drawn through the points of intersection will bisect AB. This method can be employed to divide the arc into any number of even parts by repetition. Further, the method may be used to find the centre of any given arc by further bisecting AC and CB.

Lines taken through the intersecting points of these latter arcs, when produced, will intersect at the centre of the arc AB.

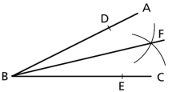
18.8E Bisecting an Angle

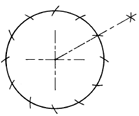
Given an angle ABC, set off equal distances BD and BE and with D and E as centres and a compass set at any reasonable radius, describe arcs to intersect in F. A line drawn through B and F bisects the angle.

18.8F Dividing a Circle into Six Equal Parts

Set a compass to the radius of the circle and step this distance off along the circumference. Further division into 12 parts may be done by bisecting one part, and again stepping off with the radius of the circle

18.8G Developing the Frustrum of a True Cone

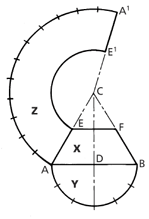
Draw the elevation X with base diameter AB, the vertical height CD to the desired cone angle and add the section line EF to the elevation. With centre D and radius DA describe a semicircle Y on the base, and divide the circumference of this into six equal parts.

To draw the development Z: With centre C and radius CB, describe an arc AA¹ whose length equals the circumference of cone base.

This may be obtained by marking off along the arc from A spaces equal to parts in the semicircle Y but double in number.(12)

With C as centre and radius CE, draw the arc EE1 and add the line CA¹.

The figure AA1E1E is the development Z of the frustrum.

To do this, drop a perpendicular from F to F¹ and extend the base line AB.

An offset diagram is now made by measuring distances B¹F¹, B¹G, and B¹H, setting these off from F¹ on base line AB and drawing lines to F.

The lengths FF¹, FG, and FH, etc., are now true lengths.

To draw the development Z:

Draw a centre line C¹O. At right angles to C¹ draw A²B² equal to AB.

From C1, set off distance C1F1, equal to FB.

Join A² and B² to F¹. With centre A² and radius F¹G, draw a short arc to be cut by an arc of F¹G radius struck from F1 to obtain point G1.

Similarly, with A² as centre and radius FH, draw an arc, to be cut by an arc of GH radius struck from point G¹, thus obtaining point H¹.

Draw a line through, A² and H¹ and produce same to intersect the centre line C¹O at O.

Repeat the process with. B² as centre for long radii, thus completing one quarter of the whole development.

To complete the pattern, draw a curve through points H¹G¹F¹ and repeat in the other sections of the development.

18.8H Developing a Square Base to a Circular Top

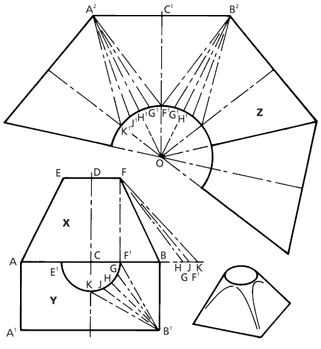
Draw the elevation X, making the base AB, vertical height CD, and diameter of top EF.

Draw a half plan Y on the base, drawing the semicircle E1F1 and dividing one half of this into a number of equal parts, F¹G, GH, HJ, and JK.

Through points F¹, G, H, J, and K, draw lines to B¹.

Before proceeding to the development it is necessary to find the true lengths of B¹K, B¹J, B¹H, B¹G, and B¹F¹.