Access the Code of Practice online

This registration will be required once-only per browser/device, which is achieved using a cookie stored on your device.

There is no password required, and your information will not be shared with any third parties.

Please register and accept the terms for the NZMRM online COP

First Name *

Last Name *

Email *

Accept Terms

By ticking this box you confirm that you have read and accept the Terms listed below

Disclaimer

Although the information contained in this Code has been obtained from sources believed to be reliable, New Zealand Metal Roofing Manufacturers Inc. makes no warranties or representations of any kind (express or implied) regarding the accuracy, adequacy, currency or completeness of the information, or that it is suitable for the intended use.

Compliance with this Code does not guarantee immunity from breach of any statutory requirements, the New Zealand Building Code or relevant Standards. The final responsibility for the correct design and specification rests with the designer and for its satisfactory execution with the contractor.

While most data have been compiled from case histories, trade experience and testing, small changes in the environment can produce marked differences in performance. The decision to use a particular material, and in what manner, is made at your own risk. The use of a particular material and method may, therefore, need to be modified to its intended end use and environment.

New Zealand Metal Roofing Manufacturers Inc., its directors, officers or employees shall not be responsible for any direct, indirect or special loss or damage arising from, as a consequence of, use of or reliance upon any information contained in this Code.

New Zealand Metal Roofing Manufacturers Inc. expressly disclaims any liability which is based on or arises out of the information or any errors, omissions or misstatements.

If reprinted, reproduced or used in any form, the New Zealand Metal Roofing Manufacturers Inc. (NZMRM) should be acknowledged as the source of information.

You should always refer to the current online Code of Practicefor the most recent updates on information contained in this Code.

Scope

This Code of Practice provides requirements, information and guidelines, to the Building Consent Authorities, the Building Certifier, Specifier, Designer, Licensed Building Practitioner, Trade Trainee, Installer and the end user on the design, installation, performance, and transportation of all metal roof and wall cladding used in New Zealand.

The calculations and the details contained in this Code of Practice provide a means of complying with the performance provisions of the NZBC and the requirements of the Health and Safety at Work Act 2015.

The scope of this document includes all buildings covered by NZS 3604, AS/NZS 1170 and those designed and built under specific engineering design.

It has been written and compiled from proven performance and cites a standard of acceptable practice agreed between manufacturers and roofing contractors.

The drawings and requirements contained in this Code illustrate acceptable trade practice, but recommended or better trade practice is also quoted as being a preferred alternative.

Because the environment and wind categories vary throughout New Zealand, acceptable trade practice must be altered accordingly; in severe environments and high wind design load categories, the requirements of the NZBC will only be met by using specific detailing as described in this Code.

The purpose of this Code of Practice is to present both Acceptable Trade Practice and Recommended Trade Practice, in a user-friendly format to ensure that the roof and wall cladding, flashings, drainage accessories, and fastenings will:

comply with the requirements of B1, B2, E1 E2 and E3 of the NZBC;
comply with the design loading requirements of AS/NZS 1170 and NZS 3604 and with AS/NZS 1562;
have and optimised lifespan; and
be weathertight.

COP v24.12:Useful-Information; Cricket-Penetration-Patterns

Cricket Penetration Patterns

18.7 Cricket Penetration Patterns

When cricket and diverter penetration flashings are used, the pitch of the cricket valley will always be less than the pitch of the roof.

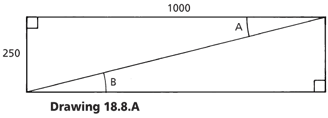
To find the pitch of a roof or valley, a simple method is to use a 1m long level measuring stick and measure the rise as shown in drawing 18.7A Measuring Stick Method. The relationship between the rise and the horizontal distance is known as the tangent of the angle and is calculated by using tan f = O/A (being the opposite side divided by the adjacent side). See 18.2 Pitch & Rise Calculator.

18.7A Measuring Stick Method

250/1000 = 0.25 = 14° (1 in 4)

N.B. Angles A and B are equal.

It is possible to obtain the length of the hypotenuse by using √ a2 + b2

Cricket flashings as described in section 6 can be made to suit any penetration width, any cricket flashing depth to width ratio and roof pitch down to 3°. For simplicity, three angles have been selected.

f X = 45°
f Y = 27°
f Z = 18°

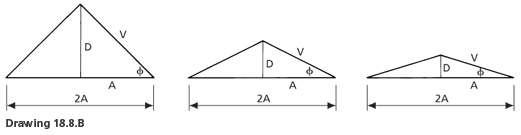
VARIATION OF CRICKET VALLEY DESIGN DEPENDENT ON DEPTH AND ROOF PITCH

Penetration Width = 2A
Depth = D
Valley = V

18.7B Cricket Variations

f X = 45°
D = A
V = √2 = 1.42

f Y = 27°
D = 1/2A
V = √1.25 = 1.118

f Z = 18°
D = 1/3A
V = √1.11 = 1.054

To find the cricket valley pitch when the roof pitch is known, it is necessary to find the depth (D) of the cricket. If the depth of the cricket is half of the width of the penetration, as shown for 'Cricket X' the angles are at 45° and there is a defined relationship between the length of the valley of the cricket and the width of the penetration and also between the pitch of the valley of the cricket and the pitch of the roof.

This is 1 : √ 2 = 1.42, which means that to maintain the desired 3° fall in the cricket valley, the minimum roof pitch (4°) can be calculated using table 15.8.

If the depth of the cricket is a quarter or a sixth of the width of the penetration, there are also defined relationships between the pitch of the valley of the cricket and the pitch of the roof.

These are described in table 18.7C Relationships between the pitch of the valley of the cricket and the pitch of the roof as 'Cricket Y' and 'Cricket Z'.

All figures comply with the minimum fall of 1.5°, but all the bold figures will provide a 3° cricket valley pitch. This methodology is valid for all sizes of penetration. However, there is a point at which, having a design with a wide penetration and a low pitch, it becomes uneconomic to pursue the ideal 3° fall in the cricket valley. When the roof pitch is known, the minimum allowable fall of the cricket valley pitch (1.5°) can then be read from table 15.8.

It is permissible to lower the valley pitch because 1.5° allows sufficient fall to clear debris from the valley and therefore qualifies as a warrantable flashing.

A diverter flashing without a cricket design only shifts the position of the cricket to the top over-flashing of the penetration as shown on drawing 9.7.6B Cricket Flashings, unless the penetration is rotated 45° as shown on drawing 9.7.6C Diverter Flashings.

18.7C Relationships between the pitch of the valley of the cricket and the pitch of the roof

ROOF PITCH	3°	4°	5°	6°	7°	8°	9°	10°
TANGENT	.0524	.0699	.0875	.1051	.1228	.1405	.1584	1763
CRICKET X	2°	3°	3.5°	4.5°				10°
CRICKET Y	1.5°	1.75°	2.25°	2.75°	3.25°	8°	9°	10°
CRICKET Z	n/a	n/a	1.5°	2°	2.25°	2.5°	3°	3.5°

PROCEDURE TO MAKE A HALF PATTERN FOR A CRICKET PENETRATION FLASHING

Example:
A net penetration width is 550 mm wide and gross width to the flat of the pans is 620 mm (2A).
The back curb is required to have a fall of 3°.
The roof pitch is 7°.
From Table 18.7C Relationships between the pitch of the valley of the cricket and the pitch of the roof . select the cricket - Type Y

Given:

Half the width of the cricket
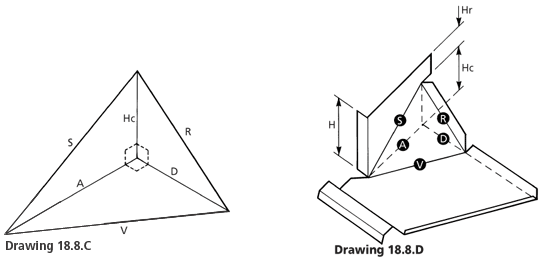
Depth of the Y cricket from drawing 15.8.B (D=1/2A)
Height of the side curb
Height to the top of the cricket
H - Hc = Hr
From Drawing 15.8.C
Find the length of V, S and R.
Right angle triangle, therefore, the length of V.

A = 310mm
D = 155mm
H = 130mm
Hc = 70mm
Hr = 60mm

V = √ A2 + D2
A = 346 mm

Right angle triangle, therefore, the length of R.

Right angle triangle, therefore, the length of S.

R = √ Hc² + D²

R = 170 mm

S = √ A² + Hc²

R = 318 mm

18.7D Cricket Pattern

DRAW A HALF PATTERN

1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.

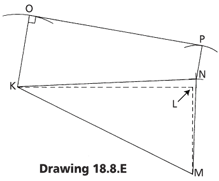
Draw a dotted line K - L length equal to A
From L draw a dotted line at right angles L - M length equal to D
Draw the line K - M (length equal to V)
With centre M scribe an arc length equal to R
With centre K scribe an arc length equal to S
From their point of intersection, N draw a line to K and also to M
With centre K scribe an arc length equal to H.
With centre N scribe an arc length equal to Hr.
Draw a line as a tangent to the two arcs
From point K, draw a line at right angles to intersect this line at O.
From O measure length A to a point P
The shape K-M-N-P-O is the net cricket pattern